How To Calculate Vessel Depressurization Time With Quick & Simple Logic
VMAC recently received a message from a process engineer in London who had a great question after reading our How to Work Out ‘Time To Fill’ Type Questions Using Simple Logic article. The process engineer asked:
“I was wondering if you have a similar calculation that you could share for “How to Calculate the Depressurization Time”? For instance, I have a pipe section at a certain pressure, and I depressurize it to a certain lower pressure through a 1” hole via a 1” valve. How long would the pipe section take to reduce pressure from P1 to P2?”
Let’s look at how we can calculate vessel depressurization time using minimal math with quick and simple logic.
Before we get started, it’s important to note we’re working in estimates to get a general understanding of depressurization time. There’s a time and place for very precise measurements but these types of physical world scenarios are rarely it. Instead, we are trying to solve a specific problem efficiently with information that’s accurate enough to move forward with an educated viewpoint.
How Quickly Does Compressed Air Escape at Various Pressures?
The following information continues on from the How to Work Out ‘Time To Fill’ article—if you haven’t had a chance to read it, check it out and then come back here. There are a few important concepts covered in that post:
- The idea that air is a spring
- How to work out the volume of a pipe
- The importance of working in psia (psig+15) when doing “air spring” calculations
Building on this background knowledge, the only new information you need to calculate depressurization time is how fast compressed air will escape out of a vent valve at different pressures.
Flow Through A Sharp-Edged Orifice – ¼” Valve
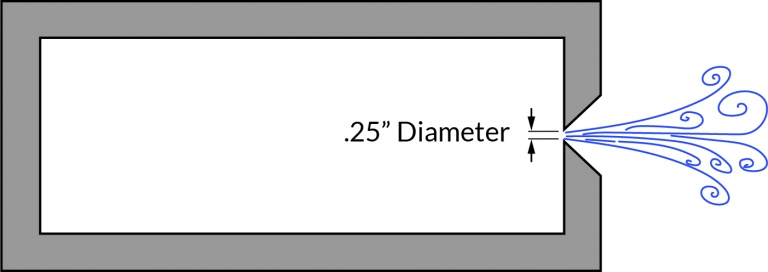
Figure 1: Vessel with 1/4″ sharp-edged orifice
| Gauge Pressure In Vessel (PSIG) | 10 | 25 | 50 | 100 | 150 |
| Free Air CFM Out Of ¼” Orifice | 17 | 30.5 | 50 | 88.5 | 127 |
A ball valve used for venting will follow the specs in the chart above if the plumbing is kept very short. This can be done by screwing a ball valve onto a nipple that’s in turn screwed into a weld-on flange or other port in the wall of the vessel being vented.
For other orifice sizes, the CFM will increase or decrease based on the increase or decrease of the orifice area. Let’s look at a 1” standard bore ball valve that’s wide open and screwed onto a 1” schedule 40 pipe nipple with a standard valve bore of 0.75”.
The orifice Area is proportional to diameter squared, which means a ¾” orifice is significantly larger than a ¼” orifice. We can calculate the ratio between the two using simple math:
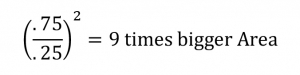
Now that we know the difference in size, we multiply the free air CFM by that difference. In this case, we’re multiplying the free air CFM by 9.
Flow Through A Sharp-Edged Orifice – 1” Valve
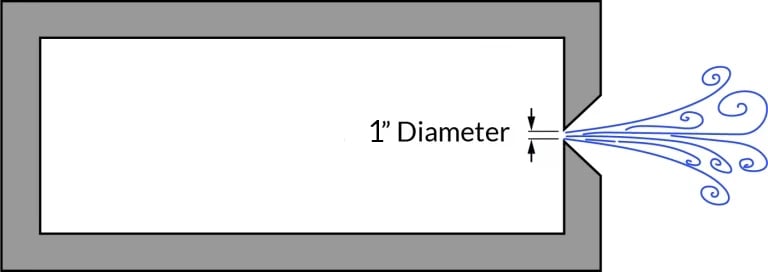
Figure 2: Vessel with 1″ sharp-edged orifice
| Gauge Pressure In Vessel (psig) | 10 | 25 | 50 | 100 | 150 |
| Free Air CFM Out Of 1” Orifice | 153 | 275 | 450 | 795 | 1145 |
Calculating Atmospheric Air Before & After Depressurization
Now that we know how quickly the air will escape, we can use some straightforward math to answer the original question: how long will compressed air take to depressurize? Let’s do an example using our 1” vent valve with a 1-mile long section of 6” pipe being vented down from 100 psig to 10 psig.
From the “Time to Fill” blog, we know that the volume of this pipe is approximately 1,000 cubic feet. We can use this to determine how much air is in the pipe before and after depressurization.
At 100 psig (115 psia), there is 7,700 cubic feet of atmospheric air packed into the pipe:
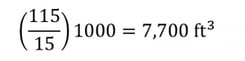
At 10 psig (25 psia), there is 1,700 cubic feet of atmospheric air packed into the pipe: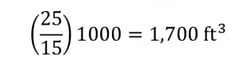
We quickly determined that we need to vent 6,000 cubic feet of atmospheric air by subtracting the cubic feet of the depressurized state from the pressurized state.
Estimating The Escape Time of Air
The quickest way to estimate how many cubic feet will escape per minute is to refer back to our depressurization chart and take the average of the outflow rate at 100 psig and 10 psig: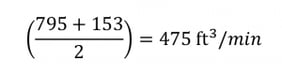
Now that we have the depressurization rate and the outflow rate, we can answer our initial question: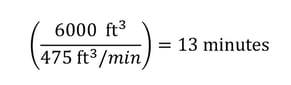
Of course, for a solution that’s a little more accurate but also more work, we would need to step the pressure from 100 to 75 psig, 75 to 50 psig, and so forth, and then add up the times required for each step.
